Define Rational Exponents and Give Examples
29
RATIONAL EXPONENTS
Fractional exponent
Exponential form vs. radical form
![]()
Negative exponent
Evaluations
The rules of exponents
![]()
BY THE CUBE ROOT of a, we mean that number whose third power is a.
Thus the cube root of 8 is 2, because 23 = 8. The cube root of −8 is −2 because (−2)3 = −8.
![]() is the symbol for the cube root of a. 3 is called the index of the radical.
is the symbol for the cube root of a. 3 is called the index of the radical.
In general,
![]() means b n = a..
means b n = a..
Equivalently,
![]()
Read![]() "The nth root of a."
"The nth root of a."
For example,
![]() -- The 4th root of 81 -- is 3
-- The 4th root of 81 -- is 3
because 81 is the 4th power of 3.
If the index is omitted, as in ![]() , the index is understood to be 2.
, the index is understood to be 2.
| Example 1. | | = | 11. |
| | = | 2 because 25 = 32. | |
| | = | 10 because 104 = 10,000. | |
| | = | −2 because (−2)5 = −32. | |
We see that, if the index is odd, then the radicand may be negative. But if the index is even, the radicand may not be negative. There is no such real number, for example, as ![]() .
.
Problem 1. Evaluate each the following -- if it is real.
| a) | | = | 3 | b) | | = | −3 | c) | | = | 2 |
| d) | | = | Not real. | e) | | = | −5 |
| f) | | = | 1 | g) | | = | Not real. | h) | | = | −1 |
| Problem 2. Prove: | 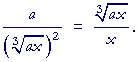 |
| Hint: Multiply numerator and denominator by | |
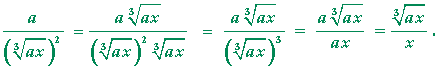
Fractional exponent
We have seen that to square a power, double the exponent.
(a 4)2 = a 8.
Conversely, then, the square root of a power will be half the exponent. The square root of a 8 is a 4; that of a 10 is a 5; that of a 12 is a 6.
This wil[l hold for all powers. The square root of a 3 is a ![]() . That of a 5 is a
. That of a 5 is a ![]() . And especially, the square root of a 1 is
. And especially, the square root of a 1 is ![]() .
.
In other words, ![]() is equal to
is equal to ![]() .
.
![]() =
= ![]() .
.
Similarly, since the cube of a power will be the exponent multiplied by 3—the cube of a n is a 3n —the cube root of a power will be the exponent divided by 3. The cube root of a 6 is a 2; that of a 2 is a ![]() . And the cube root of a 1 isa
. And the cube root of a 1 isa ![]() .
.
a ![]() =
= ![]() .
.
This is a general rule:
![]() =
=![]()
The denominator of a fractional exponent
is equal to the index of the radical.
The denominator indicates the root.
8![]() is the exponential form of the cube root of 8.
is the exponential form of the cube root of 8.
![]() is its radical form.
is its radical form.
Problem 3. Evaluate the following.
| a) | 9 | b) | 16 | c) | 25 | ||
| d) | 27 | e) | 125 | f) | (−125) | ||
| g) | 81 | h) | (−243) | i) | 128 | ||
| j) | 16 .25 =16 | ||||||
Problem 4. Express each radical in exponential form
| a) | | b) | | = | | c) | | = | (−32) |
![]()
a ![]() is the cube root of a 2. The exponent 2 has been divided by 3. However, according to the rules of exponents:
is the cube root of a 2. The exponent 2 has been divided by 3. However, according to the rules of exponents:
a ![]() = (a 2)
= (a 2)![]() = (a
= (a ![]() )2.
)2.
That is,
![]()
For example,
8![]() = (8
= (8![]() )2 = 22 = 4.
)2 = 22 = 4.
8![]() is the cube root of 8 squared.
is the cube root of 8 squared.
Again:
The denominator of a fractional exponent
indicates the root.
Although 8![]() = (82)
= (82)![]() , to evaluate a fractional power it is more efficient to take the root first, because we will take the power of a smaller number.
, to evaluate a fractional power it is more efficient to take the root first, because we will take the power of a smaller number.
In general,
![]()
Problem 5. Evaluate the following.
| a) | 27 | b) | 4 | |
| c) | 32 | d) | (−32) | |
| e) | 81 | f) | (−125) | |
| g) | 9 | h) | (−8) | |
Problem 6. Express each radical in exponential form.
| a) | | b) | | c) | | ||
| d) | | e) | | f) | | ||
Negative exponent
A number with a negative exponent is defined to be the reciprocal of that number with a positive exponent.
a −v is the reciprocal of a v.
Therefore,
| 1 | = | 1 | = | |
Problem 7. Express each of the following with a negative exponent.
| a) | 1 | = | 1 x | = | x | b) | 1 | = | x | |
| c) | 1 | = | 1 x | = | x | d) | 1 | = | x | |
Problem 8. Express in radical form.
| a) | | = | | b) | | = | 1 | |
| c) | | = | | d) | | = | | |
Evaluations
In the Lesson on exponents, we saw that −24 is a negative number. It is the negative of 24.
For, a minus sign signifies the negative of the number that follows. And the number that follows the minus sign here, −24, is 24.
[(−2)4 is a positive number. Lesson 13.]
Similarly, then,
−8![]() is the negative of 8
is the negative of 8![]() :
:
−8![]() = −22 = −4.
= −22 = −4.
(−8)![]() , on the other hand, is a positive number:
, on the other hand, is a positive number:
(−8)![]() = (−2)2 = 4.
= (−2)2 = 4.
Problem 9. Evaluate the following.
| a) | 9−2 | = | 1 92 | = | 1 81 | b) | 9 | = | 3 | c) | 9 | = | 1 3 |
| d) | −9 | = | −3 | e) | −92 | = | −81 | f) | (−9)2 | = | 81 | |||
| g) | −9−2 | = | − | 1 81 | h) | (−9)−2 | = | 1 81 | i) | −27 | = | −9 | ||
| j) | (−27) | = | 9 | k) | 27 | = | 1 9 | l) | (−27) | = | 1 9 |
| Problem 10. Evaluate | 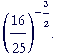 |
It is the reciprocal of 16/25 -- with a positive exponent.
So it is the square root of 25/16, which is 5/4, then raised to the 3rd power: 125/64.
The rules of exponents
An exponent may now be any rational number. Rational exponents u, v will obey the usual rules.
Example 3. Rewrite in exponential form, and apply the rules.
| = | x | |
| = | x | |
| = | x | |
See Skill in Arithmetic, Adding and Subtracting Fractions.
Problem 11. Apply the rules of exponents.
Problem 12. Express each radical in exponential form, and apply the rules of exponents.
We can now understand that the rules for radicals -- specifically,
![]()
-- are rules of exponents. As such, they apply only to factors.
Problem 13. Prove:![]()
![]() = (ab)
= (ab)![]() = a
= a ![]() ·b
·b ![]() =
= ![]() ·
·![]()
![]()
To solve an equation that looks like this:
| x | = | b, |
| take the inverse -- the reciprocal -- power of both sides: | ||
| (x | = | b |
| x | = | b |
For,x ![]() ·
·![]() =x 1 = x.
=x 1 = x.
Problem 14. Solve for x.
| a) | x | = | 8 | b) | x | = | −32 | ||||||
| x | = | 8 | = | 4 | x | = | (−32) | = | −8 | ||||
| c) | (x − 1) | = | 64 | d) | x 7 | = | 5 | |||
| x − 1 | = | 64 | x | = | | |||||
| x | = | 256 + 1 = 257 | ||||||||
| e) | x | = | 7 | f) | | = | 5 | ||
| x | = | 75 | x | = | 5 | ||||
Next Lesson: Complex numbers
Table of Contents | Home
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2021 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com
Define Rational Exponents and Give Examples
Source: https://themathpage.com/Alg/rational-exponents.htm
0 Response to "Define Rational Exponents and Give Examples"
Post a Comment